Mathematical Discourse & Our Students
by Bria Pepe
[T]here is frequently more to be learned from the unexpected questions of a child than the discourses of men, who talk in a road, according to the notions they have borrowed and the prejudices of their education.
—John Locke, Some Thoughts Concerning Education, 1693
When John Locke wrote these words at the close of the seventeenth century, the world was in the midst of the Enlightenment and change was in the air. Mary and Edward Clarke, Locke’s friends and fellow aristocrats, began seeking his advice on educating their eldest son, who was not having much success with what was then considered a typical education for boys of his class. Locke’s advice was long and specific, but he elevated virtue, a love of learning, and practicality above all. He warned the Clarkes that any tutor they found for their son should “not so much to teach him all that is knowable, as to raise in him a love and esteem of knowledge.” Locke also spoke of a child’s curiosity and how to “keep it active and vigorous” through acknowledging and answering their questions and taking seriously that which interests them. By the end of the eighteenth century, Locke’s influence on educational theory was well known and well regarded.
Hints of Locke’s beliefs on education can be found in the 1961 report issued by the National Council of Teachers of Mathematics (NCTM), The Revolution in School Mathematics. In the report, the NCTM attempted to promote the adoption of New Mathematics in American schools, a main tenet of which was discovery learning, where the “teacher must be an expert interrogator.” There were regional conferences held where panelists of teachers described their classroom experiences in the new teaching methods, and student responses were considered favorable. One telling response mirrored Locke’s advice that “children’s enquiries are not to be slighted”:
Students who had gone unnoticed before were thrilled because for once they were allowed to ask “off-beat” questions or to disagree with accepted reasons for doing things. They were allowed to find the answers for themselves.
NCTM continued to emphasize the importance of problem solving in their 1980 publication An Agenda for Action. In this iteration of their recommendations, the fundamentals of problem-solving ability are identified as “an open mind, an attitude of curiosity and exploration, the willingness to probe, to try, to make intelligent guesses.” Reference was made to providing opportunities for students “to learn communication skills” and to talk about math with “clarity.” Indeed, the recommendations explicitly noted that a mathematics curriculum that focused on problem solving should challenge all students, and “should present the opportunity for students of all levels to make a contribution.”
Based on my experiences as a public-school student in New York City and Long Island in the ‘80s and ‘90s, it would seem that the recommendations of the NCTM went unheard. My classes were tracked, and students with special needs were relegated to rooms I would never see. Although I can’t be sure how the curriculum I experienced was different from theirs, I do know that the makeup of our classrooms was based on the results of standardized testing. My peers and I were expected to discuss mathematical findings and to collaborate, uncomfortable as that sometimes was. Problem solving was an integral part of our learning, and it was hard! Despite our occasional discomfort, we rose to the expectations set by our teachers.
In Principles to Actions (2014), the NCTM extended their position on the importance of problem solving, reasoning, and utilizing effective student communication by naming high-impact mathematics teaching practices. These practices are meant to provide a foundation for strengthening the teaching and learning of math, and mathematical discourse is central to meaningful learning. Needless to say, facilitating meaningful discussion among students across both the general education and special education populations is difficult! A culture of discourse, where the teacher is an expert facilitator, must be built day by day. Smith and Stein (2011) describe five practices, commonly referred to as “The Five Practices”, that teachers can use to maximize discourse during whole-class instruction:
- Anticipating students’ solutions to a mathematics task before the lesson begins
- Monitoring students’ in-class, “real-time” engagement with the task
- Selecting approaches and students to share them with the entire class
- Sequencing students’ presentations in a specific order
- Connecting students’ approaches and the key mathematical ideas
My co-teacher and I integrate the first practice, Anticipating, before lessons by doing the same math problems our students will work on solving. Sitting next to each other during a planning period, we use our own workbooks, pencils—and, when needed, calculators—and set to work just as our students will. Then, we share our results with each other. Time and again, we’ve found that our brains approached the task differently: We each utilized different strategies to solve the same problem. We, just like our students, choose different answers for different reasons. The process of anticipating student responses is best done authentically. When we discuss our work, we also strive to come up with additional possible solutions and responses, consulting the teacher’s guide as we go.
During this same practice, we also take time to discuss Sequencing and Connecting. We make decisions about which strategies we’ll ask particular students to share and in which order, and we look to the synthesis of the lesson for how best to connect our students’ approaches to the key mathematical ideas in the lesson and beyond.
Asking students to dig deep and come up with their own mathematical ideas can be a demanding request, and many are reluctant to do so; students’ years in classrooms often start with teacher modeling, so it’s not surprising they hesitate to share their own thinking.
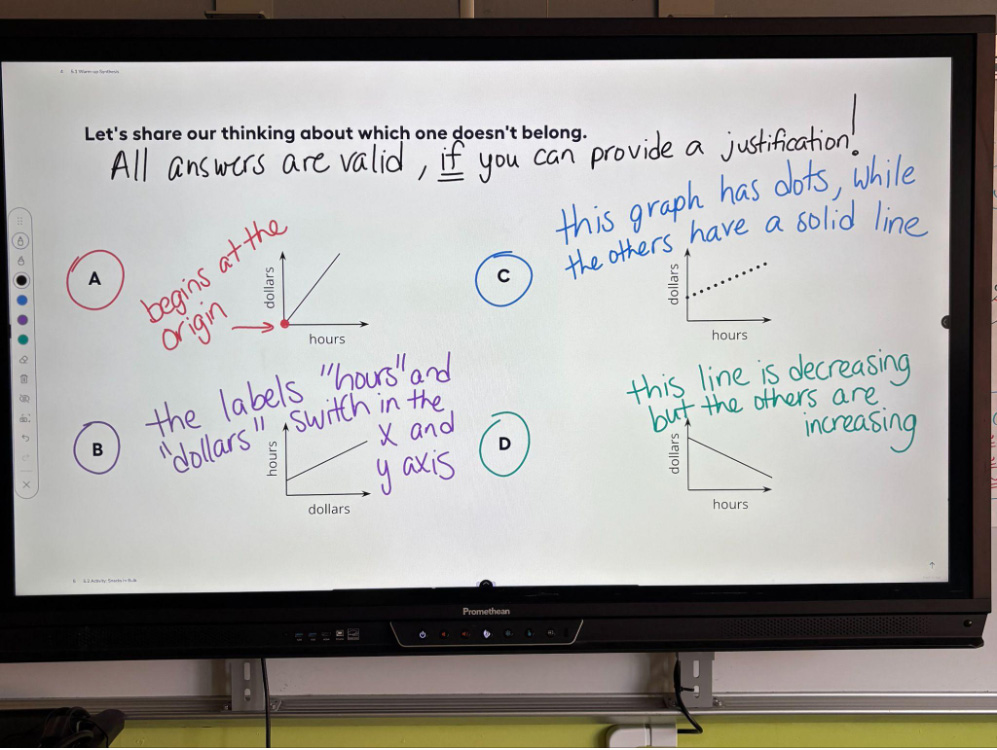
We begin our lessons by reminding students that no answer is wrong when it is supported with an accurate justification. We often start our class with a thinking routine using a puzzle from the Which One Doesn’t Belong website. Each puzzle presents four “things,” providing an opportunity to argue which one doesn’t fit with the rest as there are many correct approaches to selecting the one that doesn’t align with the others. After students spend time considering the puzzle, we invite four or five to share their ideas with the class. We’ve often found that each of the four options will be chosen by at least one student who will argue why it can be considered to not belong. And when there are options that aren’t selected, we provide some possible rationales for their differences. We document all suggestions on the board and our students note the reasons in their workbooks. Students come to see that their classroom contributions make a difference, and that they are valued mathematicians.
As students engage in problem-solving work, we positively reinforce individuals’ attempts to solve problems by marking up their workbooks with bright markers, reminding them to write down the numbers they enter into their calculators. We provide positive reinforcement by adding check marks to their written work. As we circulate, we let students know we’d like them to share their work with the class by adding stars to their papers. The process is a difficult one, but the returns are strong. When we first began this routine, we would quietly let certain students know we would be calling on them to share their amazing ideas with the class. Now, as we employ Selecting, the students expect a cold call if they receive a star. They are prepared to share, and understand that every voice has the potential to teach.
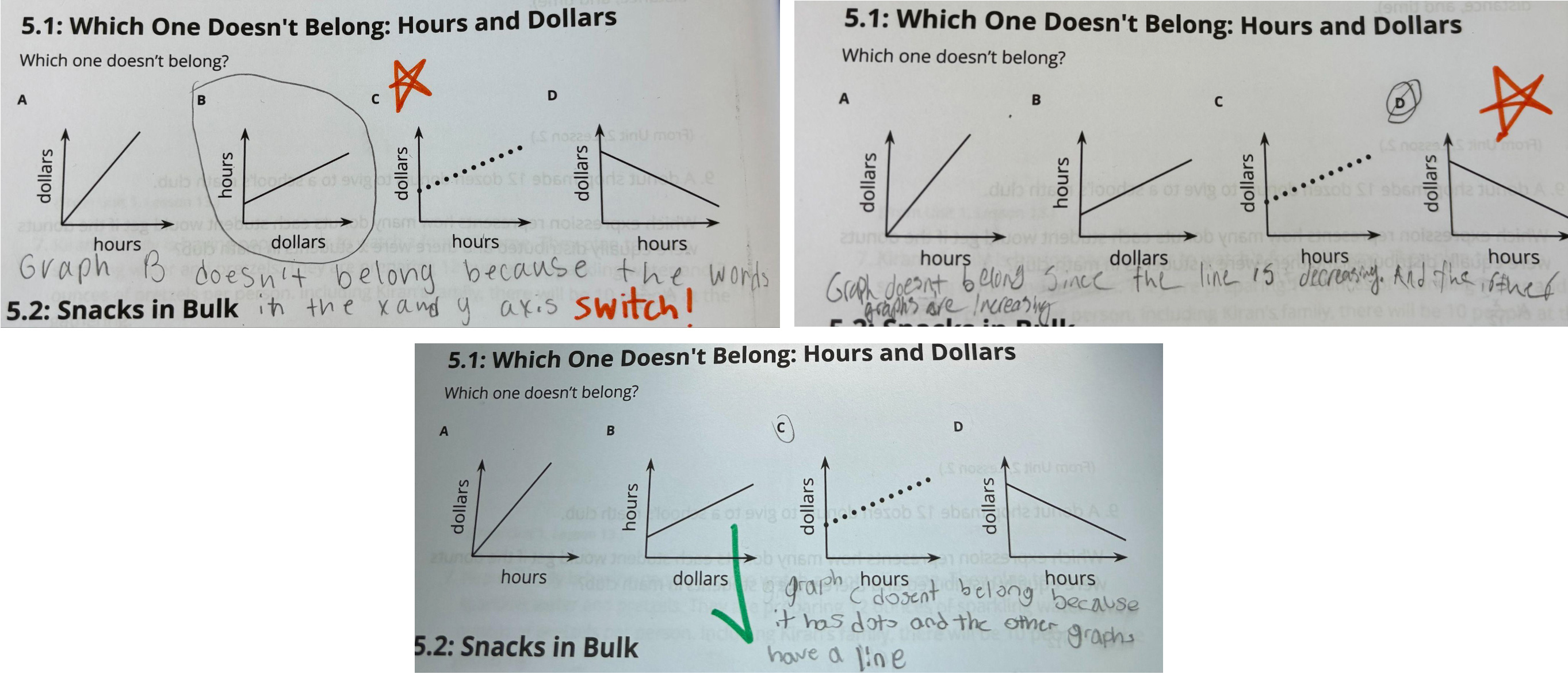
As we circulate during group discussions, we use Monitoring and encourage students who have arrived at answers to share their thinking with their peers. We’ve found that, sometimes, students who were reluctant to make a choice or attempt a solution are more likely to participate after hearing from their classmates. We reserve at least 2–3 minutes for students to share their work within their groups. When we come back together, my co-teacher and I record every comment that students share with the class, reinforcing our classroom practice of learning from each other’s ideas.
I am a special education teacher in an integrated co-teaching classroom at a public high school in a large urban district. I often struggle to make sense of the differences between my educational experience and that of my students. I hear colleagues lamenting their inclusion classrooms and bemoaning the supposed low levels of students’ achievement. We are undoubtedly challenged as we seek to support student learning for all students—those who are at, above, and below grade level. However, the strength of our communities lies in their diversity, and this holds true in our classrooms as well. Emphasizing the importance of mathematical discourse and building capacity for discourse in ALL students should be considered a means to an end: to give our students what they need to enjoy respectful and productive communication among members of the communities of which they are a part. All students, including those with learning differences, can be held to the same high standards and be engaged in rich learning opportunities. As educators, and as human beings, we owe that to them.
I’ve been teaching for almost two decades, and I’ve only begun to shift my understanding of what successful teaching and learning is. There are days when I struggle with the expectations set forth by a mathematics curriculum that elevates problem solving and student discourse, and there are days when I just want to go back to telling my students what to think and how to do it. But then I think about my daughter, Leni. As a mother, I know that I want my daughter to be a leader in her classroom. I want her questions (and there are many of them!) to be respected and valued. I want her to approach problems, both in mathematics and in life, with a can-do attitude and with confidence. If we want these things for our own children, isn’t it only right that we should do all we can to give our students the same opportunities?
References
Locke, J. (1880). Some thoughts concerning education. Cambridge University Press.
National Council of Teachers of Mathematics (NCTM). (1961). The revolution in school mathematics, a challenge for administrators and teachers.
National Council of Teachers of Mathematics (NCTM). (1980). An agenda for action: Recommendations for school mathematics of the 1980s.
National Council of Teachers of Mathematics (NCTM). (2014). Principles to actions: Ensuring mathematical success for all.
Smith, M. S., & Stein, M. K. (2011). 5 practices for orchestrating productive mathematics discussions. National Council of Teachers of Mathematics.
The contents of this blog post were developed under a grant from the Department of Education. However, those contents do not necessarily represent the policy of the Department of Education, and you should not assume endorsement by the Federal Government.
This work is licensed under CC BY-NC-SA 4.0
Math for All is a professional development program that brings general and special education teachers together to enhance their skills in
planning and adapting mathematics lessons to ensure that all students achieve high-quality learning outcomes in mathematics.
