Sign Up for Our Newsletter
Receive ideas for making high-quality mathematics instruction accessible to all students and stay connected with the Math For All community
* Indicates required fields.
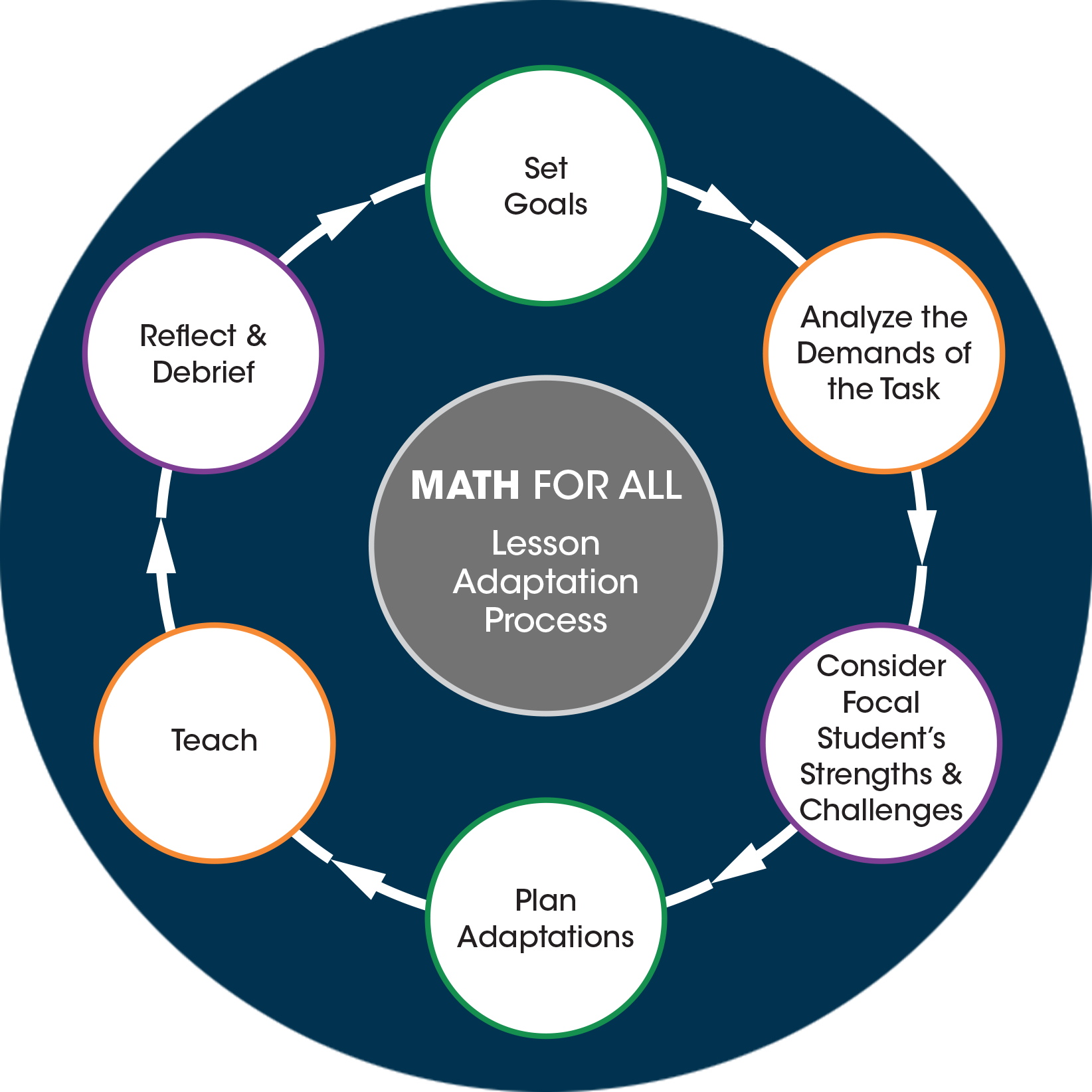
Math for All is a professional development program that brings general and special education teachers together to enhance their skills in planning and adapting mathematics lessons to ensure that all students achieve high-quality learning outcomes in mathematics.
Focus on Identified Students, Apply Strategies to
All Students