Engaging all Students: Rich Tasks and a Strengths-Based Approach
by Charlene Marchese and Andrea Brothman
Consider the following 6th-grade task from Illustrative Mathematics. Take a few moments to solve it using any method you like.
Jessica gets her favorite shade of purple paint by mixing 2 cups of blue paint with 3 cups of red paint. How many cups of blue and red paint does Jessica need to make 20 cups of her favorite purple paint?
Did you read the problem and hear yourself mutter “Hmmm…”? Were there multiple options to consider for working out a solution? Did you find yourself mulling over why one strategy was stronger than another? Could you solve this question quickly or did you need to take your time? Did you arrive at an answer?
Why Rich Tasks?
The Perfect Purple Paint problem is considered to be a rich math task, and the questions posed above get at the kinds of thinking opportunities rich tasks offer. Rich tasks require one to slow down, to think, and to reason. When students explore rich tasks in partnerships or groups, they can benefit from sharing and reflecting on their own strategies alongside hearing those of others. While rich tasks are complex, they are not categorically advanced. Carefully chosen, they can engage students in deep thinking about important grade-level concepts and standards.
Another important characteristic of rich problems is that they offer multiple points of entry, at varying levels of abstraction. Three very different approaches to the Perfect Purple Paint problem are below. Review each and see how your approach was similar to or different from the ones shown.
Approach 1: Tiles and Sentence Frames
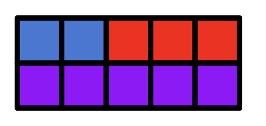 |
For every 2 cups of blue paint, 3 cups of red paint is mixed to create 5 cups of purple paint. |
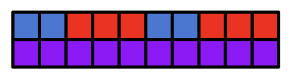 |
For every 4 cups of blue paint, 6 cups of red paint is mixed to create 10 cups of purple paint. |
 |
For every 6 cups of blue paint, 9 cups of red paint is mixed to create 15 cups of purple paint. |
 |
For every 8 cups of blue paint, 12 cups of red paint is mixed to create 20 cups of purple paint. |
Approach 2: Double Number Line
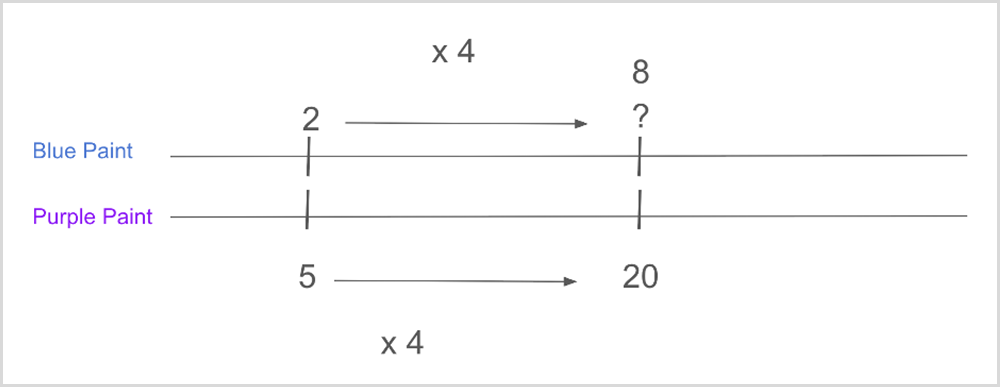
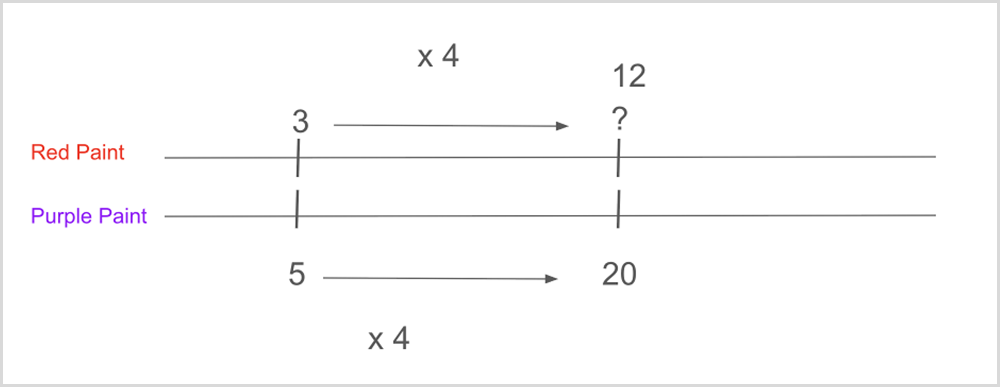
Approach 3: Ratio Table
Cups of Blue Paint |
Cups of Red Paint |
Cups of Purple Paint |
| 2 | 3 | 5 |
| 4 | 6 | 10 |
| 6 | 9 | 15 |
| 8 | 12 | 20 |
You may have used a strategy similar to one of the approaches, or perhaps you used a different one. And this is the point and beauty of rich tasks: Multiple points of entry make complex problems accessible to a wide range of students.
Higher Order Thinking Demands
In order to prepare to use this problem in class, we do the problem ourselves, hands-on, as our students would. We use Math for All’s Neurodevelopmental Framework to help identify the cognitive demands of the task, to understand the strategies our students might use, and the challenges they might face.
We see that there are multiple cognitive systems in play when solving the paint problem. In addition to language demands (understanding the words paint, cups, shade, mixing), and memory demands (recalling the question as well as the original paint ratio while working through the problem), there also are significant higher order thinking demands embedded in this task, including requiring a conceptual understanding of proportional reasoning and equivalent ratios. Conceptually, students must understand that:
- creating the same shade of purple means that you have to use the exact same proportions of blue and red paint every time, meaning that for every 2 cups of blue paint in the mixture, there always must be 3 cups of red paint;
- the cups of blue and red paint are the “parts” and cups of purple paint are the “whole;”
- when using the ratio table, skip counting is connected to multiplication.
Proportional reasoning is one of the major building blocks of algebraic reasoning, and so helping students understand it at a conceptual level is key toward understanding more advanced mathematics.
Recognizing the important role that conceptual understanding plays in this proportion problem, we must consider how to best support our students as they engage in this task. How might the three approaches presented above work for them? Are there other models they could benefit from using? Would specific students need different models or adaptations so they can also access the higher order demands of this task?
Strengths-Based Approach
In a strengths-based classroom, a variety of approaches to understanding mathematical concepts are available and students are encouraged to engage in multiple approaches. This offers students access to the problem in modalities that play to their strengths, and teachers and students together can develop an understanding of each student’s learning strengths. As students come to understand their own learning strengths they can advocate for themselves and have agency over their own learning. What a powerful lifelong learning tool!
Let’s consider how we can support students using each approach provided at the start of this blog post.
Integrate Manipulatives. Students who have strength in spatial functions may benefit from “seeing” the relationship between the two items. One support might be to secure 2 blue tiles together and also secure 3 red tiles together, making several sets of each. Combining one set of each represents the number of cups needed for 5 cups of the ideal shade of purple paint. When put together, regardless of the amount of purple paint that will result, the visual shows that the ratio of blue to red paint remains at 2:3. Manipulatives can help learners visualize the cups of paint and can offer support to students.
Use Sentence Frames. Students who have strength in language functions may benefit from a set of sentence frames such as I used ____ cups of blue paint and ____ cups of red paint to create ___ cups of purple paint. This adaptation gives students a place to record paint combinations and provides a consistent way of articulating the thinking pattern. The sentence frames also relieve students of the cognitive demands required to create the sentence structures in their heads, allowing them to focus on the content.
Offer a Double Number Line. Students who have strength in sequential functions may benefit from representing the ratios on a double number line. Double number lines can be a helpful tool for understanding and solving ratio problems as they visually represent the relationship between two quantities. Providing the number line also relieves students of having to create their own, and offers a suggested solution path.
Provide a ratio table. Students who have strength in sequential functions may benefit from documenting the ratios in a ratio table. A ratio table provides a clear space for students to organize their work and supports seeing and finding patterns (the number of cups of paint doubles with each row).
Engaging students in problem solving with rich tasks is a critical component of their mathematics education. As students apply their understanding of concepts and skills to solve a task they deepen their understanding of the content. Using an instructional approach that offers multiple access points that allow students to use their strengths can increase access to successful problem solving and build students’ conceptual understanding.
The contents of this blog post were developed under a grant from the Department of Education. However, those contents do not necessarily represent the policy of the Department of Education, and you should not assume endorsement by the Federal Government.
This work is licensed under CC BY-NC-SA 4.0
Math for All is a professional development program that brings general and special education teachers together to enhance their skills in
planning and adapting mathematics lessons to ensure that all students achieve high-quality learning outcomes in mathematics.
