Strategies for Math Intervention Can Benefit All Students
by Kate Coleman
Every math classroom is filled with students who have different strengths, experiences, and learning needs. While research-based math intervention strategies are designed to support students who struggle, these same practices can also strengthen learning for all students.
This blog post explores two powerful practices that can help students deepen their understanding of mathematical concepts: building mathematical language and using models and manipulatives (also known as representations). Language and representation might seem distinct at first, but in reality, they are constantly interacting. When students are explaining their ideas aloud or showing their thinking by using models, language and representations work together to help students make sense of math.
These practices are highlighted in the What Works Clearinghouse Practice Guide Assisting Students Struggling with Mathematics: Intervention in the Elementary Grades (Fuchs et al., 2021), and are key recommendations for offering additional support to students. But these strategies aren’t just for intervention—they are powerful tools that educators can use to create more inclusive and effective mathematics classrooms where all students can engage, communicate, and deepen their understanding (Scherer et al., 2016).
Mathematical Language
The Importance of Mathematical Language
Communicating ideas clearly and with precision is essential to constructing concepts, formulating arguments, and developing mathematical understanding. In the math classroom, communication can come in many forms—students speaking aloud to share ideas, writing to explain their reasoning, or using symbols or notations to represent ideas.
Mathematical language is more than knowing vocabulary—it includes opportunities to receive and process information through listening and reading (receptive language) as well as produce information through speaking and writing (expressive language). Supporting both is key to helping students explain their ideas, receive feedback, and refine their thinking (Bay-Williams & Livers, 2009). Educators can provide immediate feedback and address misunderstandings through targeted scaffolds that support vocabulary development (Riccomini et al., 2015). When students have regular and frequent opportunities to communicate their thinking and be actively engaged in their mathematics, they not only strengthen their own learning but also contribute to the shared understanding of the classroom community (Riccomini et al., 2015).
Strategies to Support Mathematical Language Development
Provide sentence frames or sentence starters to support student writing and talking.
Sentence frames and sentence starters are simple, effective scaffolds that help students organize and express mathematical thinking (Zwiers et al., 2017). While both can serve similar purposes—to provide a framework for providing explanations, articulating questions, and recounting information—there are subtle differences between them.
Sentence frames exclude parts of sentences, allowing students to fill in the blanks using key vocabulary or ideas, as shown in samples below:
This array has ____ rows, ____ columns, and ____ squares in all.
I can prove that ____ and ____ are equivalent fractions because ____.
Sentence starters provide the opening stem of a sentence, providing a prompt for students to complete, as shown in the samples below:
The strategy I used to solve the problem is…
I noticed a pattern when…
I agree with your idea because…
Including these supports in instruction doesn’t need to be a heavy lift. Sentence frames and starters can be printed and cut into strips for individual or small group use or even just written on chart paper or on a white board. The key is to plan ahead by identifying the mathematical vocabulary you want students to practice using. By preparing these supports in advance, you make it possible for all students to intentionally use math language and participate in meaningful conversations about their learning.
Construct a word bank with students.
A word bank is a collection of terms aligned to lesson content that helps students access and use words with precision. Word banks can include content specific terms, like “area” or “ratio,” as well as academic words that students may use across subjects, like “table”, “calculate” or “construct.”
Instead of providing students with a pre-made list, consider co-constructing a word bank. Building the word bank with students activates their prior knowledge and encourages them to be intentional about using the identified terms in their explanations. Creating this tool also provides students with a sense of ownership of and connection to the mathematical language.
When including a word bank, it is helpful to
- keep the word bank visible and accessible—post it on chart paper or provide copies to students;
- refer to it regularly throughout instruction and model how to use the words in context;
- revisit and expand the list as new concepts and vocabulary are introduced.
Pause, critique, correct, and clarify ideas through math language routines.
Zwiers et al. (2017) encourages the use of math language routines—structured opportunities for students to practice mathematical language in meaningful ways. One example is the Critique, Correct, and Clarify routine. In this routine, students review an anonymized version of another student’s mathematical explanation that is ambiguous or incomplete and identify ways to improve it. This routine encourages students to reflect on the mathematical strategies used, the language used to explain them, and the words that could provide a stronger explanation. Teachers can build in similar opportunities for reflection and discussion by
- pausing after introducing a new concept to give students time to process and to ask questions;
- encouraging students to respectfully critique a partial response or a misunderstanding (Zwiers et al., 2017);
- facilitating Think-Pair-Share activities where students can verbalize their thinking before sharing with the larger group.
These strategies give students a chance to practice using mathematical language in a supportive environment. These moments for reflection and discussion help students to integrate new terms into their mathematical vocabulary while building conceptual understandings and solidifying ideas. Intentionally incorporating these strategies into lessons to build math language will support all students to develop into more confident and articulate mathematicians.
Using Representations to Visualize Concepts
The Role of Representations
Just as students need opportunities to talk about and explain their mathematical thinking, they also need ways to show and visualize their ideas. Using concrete manipulatives and visual models—known as representations—helps students to make sense of their developing understandings and to strengthen their reasoning skills (Gersten et al., 2009). Providing students targeted opportunities to use a variety of representations, such as manipulatives, drawings, and diagrams, supports both their ability to communicate their thinking effectively and to develop deeper conceptual understanding (Agrawal & Morin, 2016).
One approach to using representations is the Concrete-Representational-Abstract (CRA) framework. The framework describes three types of representations that can help students engage in mathematical ideas (Agrawal & Morin, 2016):
- Concrete representations: Using physical manipulatives and objects that students can touch and move.
- Representational (or semi-concrete) representations: Creating drawings, diagrams, or visual models to represent mathematical concepts.
- Abstract representations: Using numbers, symbols, or equations to represent mathematical ideas.
While CRA is sometimes presented as a linear sequence, effective math instruction moves flexibly among all three, often using multiple types at the same time to deepen understanding (Agrawal & Morin, 2016). Students make stronger transitions to the “abstract” when they are exposed to mathematical notation alongside concrete and semi-concrete models (Agrawal & Morin, 2016; Miller, et. al, 2011). Teachers can strengthen these connections by pairing representations together, helping students move among concrete, semi-concrete, and abstract ideas, rather than treating them as sequential steps (Fuchs et al., 2021).
Strategies for Using Representations
Model strategic use of manipulatives and have students use them often.
Regular engagement with concrete materials strengthens conceptual understanding. For example, using fraction tiles to model where fractions are located on the number line helps students visualize fractional relationships and build mental models. While manipulatives offer valuable support, being strategic about how they are introduced and used makes them even more effective. Consider the following tips for doing so:
- Keep a variety of manipulatives accessible (base ten blocks, fraction tiles, etc.) and encourage their use (Fuchs et al., 2021).
- Use proportional manipulatives, like base ten blocks or fraction tiles (as shown below) wherever possible to help students see mathematical relationships clearly. (Fuchs et al., 2021).
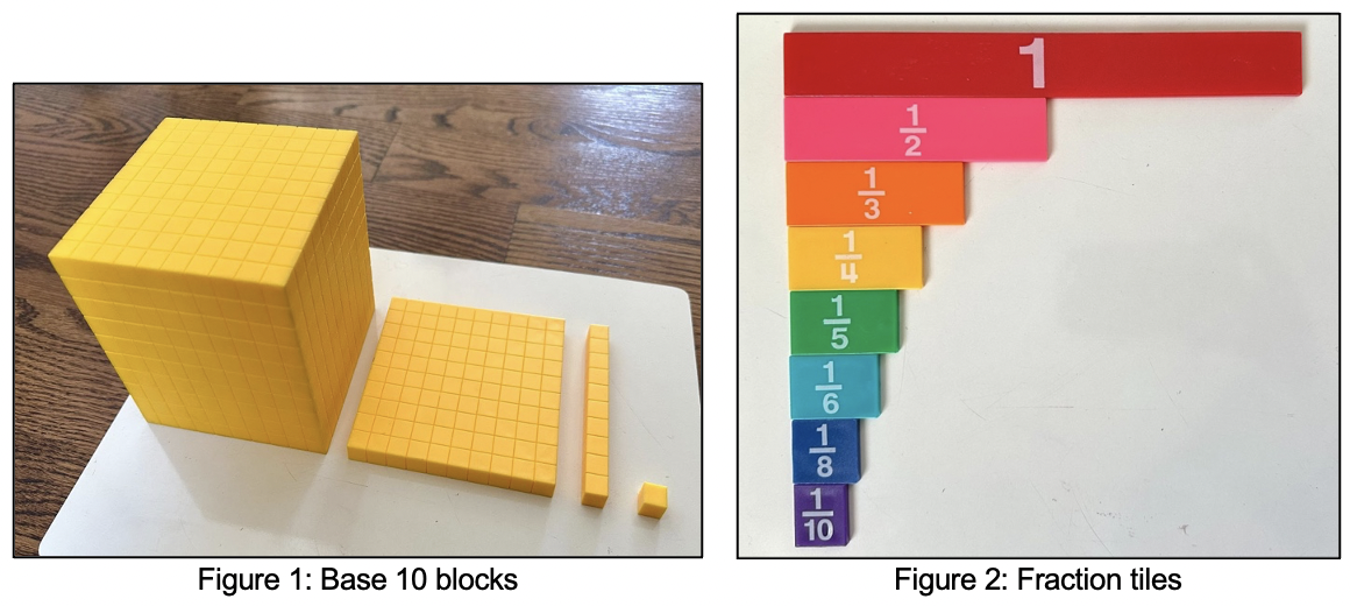
- Model how to use manipulatives to represent and solve problems, showing students how to make connections between the model and the mathematical ideas it represents (Fuchs et al., 2021).
Encourage strategic pointing and the use of color to highlight parts of a model or a diagram.
When students work with manipulatives or semi-concrete models, it is important for them to explain their thinking by referring to specific parts of the representation. This helps students clarify their ideas and connect parts of representations to the mathematical concepts they are learning. Two simple but powerful techniques to support this are:
- encouraging students to point to specific elements of a model or diagram as they explain their reasoning;
- inviting students to use colored markers or pencils to highlight parts of a model or diagram and connect it to written equations or symbols.
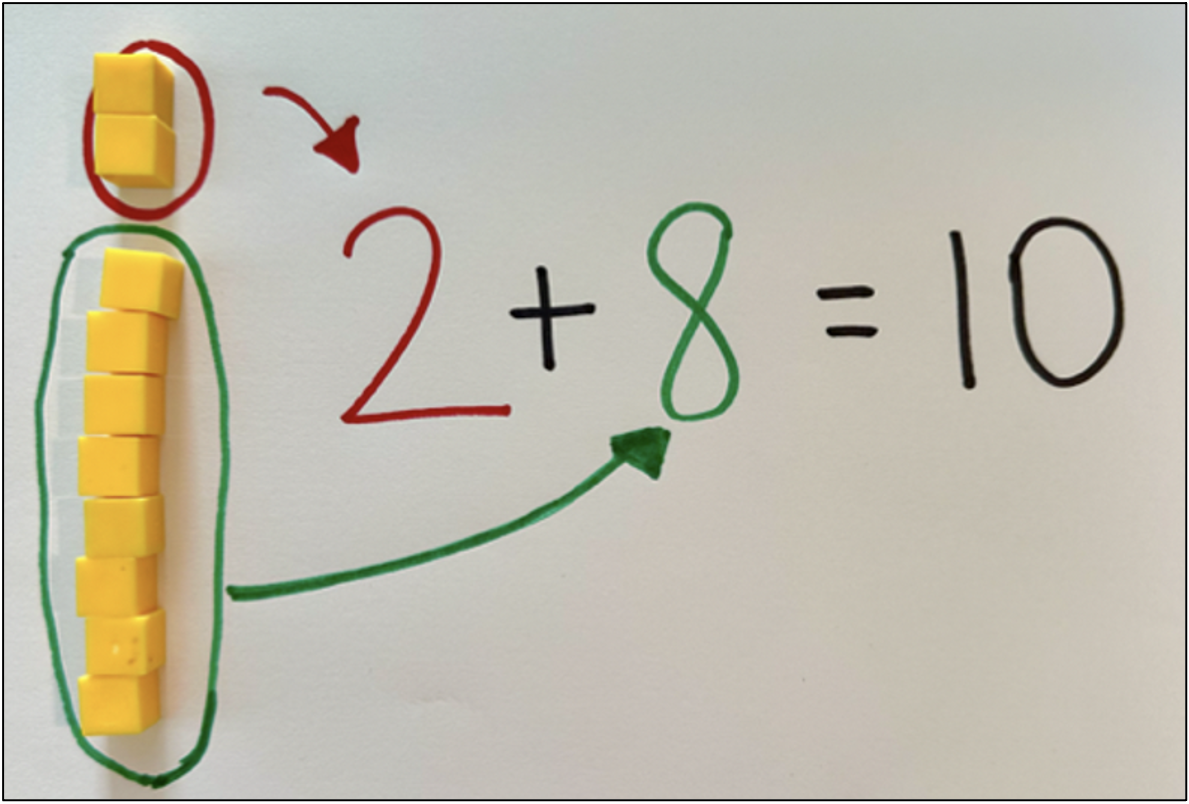
These strategies help students make their thinking visible—both for themselves and for others. Encouraging students to explain their models supports classroom discussion, deepens conceptual understanding, and strengthens the connections between concrete, semi-concrete, and abstract representations.
Classroom Implementation: Pulling It All Together
By incorporating evidence-based intervention strategies to support mathematical language and to use representations, educators can create more inclusive and effective mathematics classrooms (Orosco, 2014; Scherer et al., 2016). These approaches not only support students who may experience difficulties but enhance the learning experience for everyone, helping all students to develop deeper mathematical understanding and stronger communication skills.
Implementing these strategies doesn’t require a complete overhaul of your teaching practice. Small, intentional moves or adjustments—like providing sentence frames, co-constructing word banks, and strategically using proportional manipulatives like fraction tiles—will positively affect student understanding. When we adopt the mindset that intervention strategies can benefit all students, we expand our options for creating learning environments where all learners can access and engage with mathematics. I encourage you to choose one strategy to try in your next lesson. Your entire classroom community will benefit from small but powerful shifts in instruction.
References
Agrawal, J., & Morin, L. L. (2016). Evidence-based practices: Applications of concrete representational abstract framework across math concepts for students with mathematics disabilities. Learning Disabilities Research & Practice, 31(1), 34–44.
Bay-Williams, J. M., & Livers, S. (2009). Supporting math vocabulary acquisition. Teaching Children Mathematics, 16(4), 239–246
Colorín Colorado. (n.d.). Sentence frames and sentence starters.
Fuchs, L. S., Bucka, N., Clarke, B., Dougherty, B., Jordan, N. C., Karp, K. S., Woodward, J., Jayanthi, M., Gersten, R., Newman-Gonchar, R., Schumacher, R., Haymond, K., Lyskawa, J., Keating, B., & Morgan, S. (2021). Assisting students struggling with mathematics: Intervention in the elementary grades (WWC 2021006). What Works Clearinghouse, Institute of Education Sciences, U.S. Department of Education.
Gersten, R ., Chard, D. J., Jayanthi, M., Baker, S. K., Morphy, P., & Flojo, J. (2009). Mathematics instruction for students with learning disabilities: A meta-analysis of instructional components. Review of Educational Research, 79(3), 1202–1242.
Miller, S. P., Stringfellow, J. L., Kaffar, B. J., Ferreira, D., & Mancl, D.B. (2011). Developing computation competence among students who struggle with mathematics. Teaching Exceptional Children, 44(2), 38–46.
Orosco, M. J. (2014). Word problem strategy for Latino English language learners at risk for math disabilities. Learning Disability Quarterly, 37(1), 45–53.
Riccomini, P. J., Smith, G. W., Hughes, E. M., & Fries, K. M. (2015). The language of mathematics: The importance of teaching and learning mathematical vocabulary. Reading & Writing Quarterly, 31(3), 235–252.
Scherer, P., Beswick, K., DeBlois, L., Healy, L., & Opitz, E. M. (2016). Assistance of students with mathematical learning difficulties: How can research support practice? ZDM Mathematics Education, 48, 633–649.
Zwiers, J., Dieckmann, J., Rutherford-Quach, S., Daro, V., Skarin, R., Weiss, S., & Malamut, J. (2017). Principles for the design of mathematics curricula: Promoting language and content development. Stanford University, Graduate School of Education.
The contents of this blog post were developed under a grant from the Department of Education. However, those contents do not necessarily represent the policy of the Department of Education, and you should not assume endorsement by the Federal Government.
This work is licensed under CC BY-NC-SA 4.0
Math for All is a professional development program that brings general and special education teachers together to enhance their skills in
planning and adapting mathematics lessons to ensure that all students achieve high-quality learning outcomes in mathematics.
