Routines for Mathematical Thinking & Engagement

The beginning of the school year is filled with excitement and anticipation. There are materials to prepare and organize, lessons to plan, and classrooms to set up. As teachers, we think carefully about the norms, structures, and routines that we want to establish. Everything from housekeeping to how we communicate with each other to how we move about the classroom contribute to students feeling safe to share their thinking, take risks, and solve problems.

Thinking routines establish predictable patterns in ways of thinking and send strong messages about what is valued within the classroom community. Harvard’s Project Zero defines a thinking routine as “a set of questions or a brief sequence of steps used to scaffold and support student thinking.” In the context of mathematics, thinking routines can convey that it’s our thinking that matters, not just the answers. They can communicate that what is valued is our collective understanding, not our individual performance. Beginning a lesson with a thinking routine communicates that everyone has something to contribute, that our understanding is deepened through discourse; it is a way to ensure that every student experiences success. In contrast to a “mad minute” or other rote computational tasks that may start off a math class, the thinking routines we offer here focus on justification, flexible thinking, and clear communication.

Thinking routines are a great way to pique curiosity while being accessible to all students. Let’s take a look at a few examples of thinking routines you can use to start off your math class and set the tone for the rest of a lesson:

Notice and Wonder. This routine has become, well, quite routine in many classrooms! The power in notice and wonder lies in its accessibility to all students; all students can notice something and there are no incorrect responses to what we notice! Using visual images for a notice and wonder routine is a great way to further increase accessibility and to emphasize mathematical relationships over computation. Additionally, research supports the importance of visual mathematics for our learning. Education Development Center (EDC) has an extensive collection of images of different mobiles similar to the one below that can be used in a notice and wonder routine.

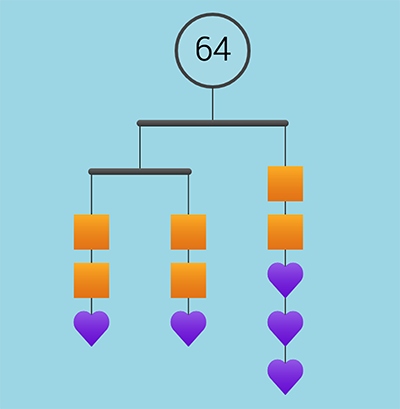
Looking at this image, what do you notice? What do you see? What does it make you wonder? What might your students see in this image, and what questions might they come up with?

Which One Doesn’t Belong? (Alternatively, Which One Is Unique?). In this routine, there are, by design, several correct answers. Students are shown four quadrants with an image in each. Their job is to decide which of the four is different from the rest. Students can justify any of the four quadrants as being unique, and therefore the emphasis of the routine is on students’ reasoning. Many examples of and inspiration for images can be found on the site “Which One Doesn’t Belong?”

Look at the four triangles in this example. How is each one unique? What reasoning might your students use to prove how each is unique? What kinds of relationships and attributes would they focus on, and what kinds of conversations might develop from what they notice?

What’s the Same? What’s Different? In this routine, students are shown two side-by-side images and are tasked with sharing what they notice about how the images are the same or different. Again, the emphasis here is on justification and reasoning, and it gives students an opportunity to practice using precise language to describe the similarities and differences. Some inspiration for images can be found on Dr. Sue Looney’s site “Same but Different Math”. What might your young students say if presented with the following image?

True or False? This routine challenges students to evaluate whether or not an equation is true or false without evaluating each side! This is a way for students to focus on the relationships between numbers rather than on computational skills. For example, how could you decide if the following equation is true or false without evaluating each side? What mathematical relationships and big ideas are you using to decide?

659 + 357 = 660 + 356

When you use these or any other thinking routines to begin your math lesson, it’s important to consider what is accessible for all students as well as which big mathematical ideas you want your students to be thinking about that day. We want all students to experience success as they begin the lesson, and these routines allow for that while also engaging students in thinking about big ideas.

All students can and should experience success every day in the math classroom. This doesn’t mean that they won’t be challenged, make mistakes, or struggle. Starting class with a thinking routine is a way to ensure success while supporting students’ ability to reason, communicate their thinking, and develop confidence in mathematics. Thinking routines ensure that every student is successfully engaged in mathematical thinking from the beginning of the lesson. Success primes students to take on the mathematical challenges and intellectual risks of the day.

What other thinking routines have you used in your classroom? We encourage you to try these and other thinking routines and notice how they influence classroom culture and learning.