Three-Act Tasks and a Neurodevelopmental Mystery
By Arjan Khalsa
Three-Act Tasks. Notice and Wonder. Estimation 180. Math Talk. We learn about these leading practices for mathematics education in publications, on social media, and during professional learning events. Many educators find that these strategies are transforming today’s classrooms through increased engagement, constructive risk-taking, and rigorous problem-solving. We may be curious: From a cognitive development viewpoint, why are these techniques so effective?
Some recent work has given me new clues to solving this mystery. Over the past few years, I have become acquainted with the Math for All project that helps classroom and special education teachers view student strengths and challenges through a neurodevelopmental lens. Students who seem to struggle with math tasks may actually be struggling with a disconnection between their learning needs and classroom teaching strategies. Here is a simplified snapshot of the neurodevelopmental functions addressed in this project:
- Attention. Does the student stay focused on tasks, process incoming information, and regulate their responses?
- Language. Does the student understand the language in the problem? Can they read it? Can they explain their thinking?
- Higher-order Cognition. Does the student engage in complex and sophisticated thinking when required?
- Memory, Social Cognition, Motor Coordination, and Sequential and Spatial Ordering are among the other functions addressed by Math for All.
It occurs to me that leading mathematical practices can effectively support students with different strengths and challenges in neurodevelopmental areas. In this article, we will look at a high-quality three-act task implemented with these leading practices. We will see how students solve their mathematical mystery as their teacher solves the teaching mystery of reaching all students in the inclusive elementary classroom.
Three-Act Tasks. Three-act tasks are dramatized mathematics investigations structured in a three-part sequence and often presented through Web-based videos. Act one is a lesson launch, typically presenting a thought-provoking phenomenon for students to observe and ponder. Act two is a period of exploration in which students request clarifying data and then answer their own questions about what they observed in the first act. Act three brings the problem to a conclusion and offers students the opportunity to reflect on their solutions.
Getting Started with Array-bow of Colors, Act One. Array-Bow of Colors is a fourth-grade three-act task published by Graham Fletcher and freely available on the Web. (Links to all referenced resources are provided below.) In Act One, students collectively watch a fascinating, fast-motion video of a person emptying small packs of Skittles candy into a large jar. Students’ immersion in the video provides the first clues to our teaching mystery. Engaging students who have attention challenges can be more successful when the task commands their attention!
Additionally, sharing a phenomenon through video can increase access for students who have strengths in visual processing but have challenges with language, especially text.
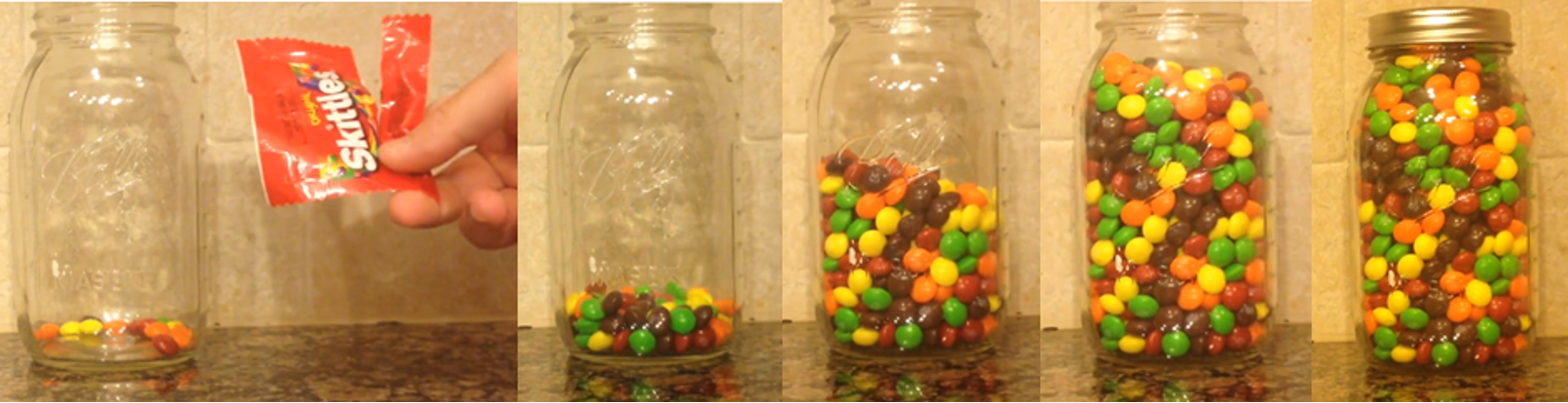
Notice and Wonder, Math Talk. This task is perfect for employing the “notice and wonder” strategy that is well-documented on the website of the National Council of Teachers of Mathematics (NCTM). The teacher poses questions to the class: “What do you notice? What do you wonder?” Students are encouraged to share their observations and engage their own curiosity to recognize intriguing problems.
Let us envision a student who has difficulty with social cognition. She states: “I noticed someone pouring Skittles into a jar.”
The teacher is versed in math talk, employing talk moves to orchestrate productive discourse, and decides to stay with this student and probe for more ideas. The teacher asks, “What else did you notice?” The student continues, “There were a lot of packages … so many Skittles in the jar!” And now we have a second clue: Intentional math talk can help students with strengths in language but who have social challenges by providing safe entry points into discourse.
The teacher asks the whole class what they notice and wonder. Students call upon their active working memory of the video. Through the use of partner talk and table talk, each student finds that their voice, and every voice, matters. Their collective wonder turns into a class mission:
We want to find out how many Skittles are in that jar!
This is student-centered learning. The students have effectively conceived their own mystery, designed their own mathematics problem. Now, they must solve it, one clue at a time!
Estimation 180. It is time to estimate, and Estimation 180 is a helpful approach for many rich math tasks. Students make three estimates, working in facilitated pairs or groups. The first estimate is reasonable yet intentionally low. The second is reasonable yet intentionally high. The third estimate represents the students’ best effort at predicting the result. A low estimate of five Skittles in the jar would not pass the “reasonable” test. A high estimate of one billion would simply be silly. So, the teacher asks the students to take responsibility and apply rigor to their estimates, ultimately recording the results for all to see.

Consider how neurodevelopmental functions are addressed through Estimation 180.
- Students can recall their estimates as they are now on the blackboard. Memory – supported.
- The three-estimate strategy gives them a framework to support thinking. Higher-order cognition – supported.
- With all students contributing to the group estimates, their social engagement is productive and safe. Social cognition – supported.
- There is excitement in the room. Which team made the best estimates? Attention – supported.
Act Two. Act Two poses the questions “How can we solve our mystery? What information will help us find out how many candies are in this jar?” As students ponder these questions, their conversation steers them toward the clues, the data, that they seek. The students decide that they would like to know how many Skittles are in one package and how many packages are in the jar.
As Act Two unfolds, students see pictures of the emptied Skittles packages and learn that there are 58 in total. They see a single package with its emptied contents on display: 14 Skittles. They now have two clues, two crucial data points: 58 packages and 14 Skittles per package. The mathematics is taking shape. As Sherlock Holmes would say, “The game is afoot!”

The C-R-A Sequence. The Concrete-Representational-Abstract sequence is a time-honored approach. In this case, the “concrete” beginnings can be seen in two ways. First, there is the video that provides a close-to-visceral experience with the candies. Second, the “C” can be interpreted as context. A strong context, a highly motivating story, can serve as the “C” in C-R-A.
Some students may not instantly know that the solution lies in multiplying 58 times 14. This is where the “R,” representation, is so important. Students draw models of what they have observed using spatial ordering to reveal the process of multiplying. Students progress to the “A,” the abstraction of multiplying, with a strong understanding of why multiplication makes sense. Act Three begins when the students have completed their calculations and are armed with their responses, still reflecting on their estimates, with most expecting there to be 812 (58 x 14) Skittles in the jar.
Act Three, Mystery Abounds! Any good mystery deserves a twist, and this task comes through. In the Act Three video, a person pours the Skittles out of the jar and, in fast motion, organizes them in a clear and colorful array, the “array-bow of colors.” Students watch in anticipation, hoping to validate their updated prediction of 812. But, alas, the total number of Skittles is different!
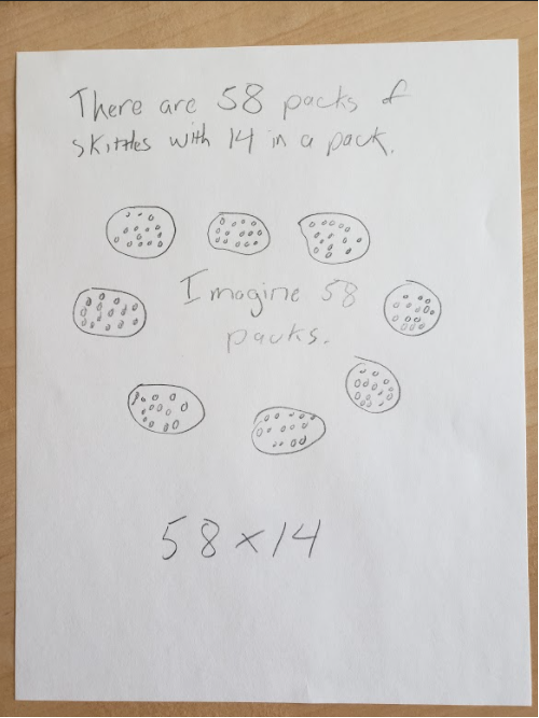
I hate to spill the beans, or spill the Skittles, and deny you and your students the delightful revelations in store. Act Three is not over yet, students have some thinking to do!
Unraveling the Twist. The Act Three twist has captured student attention. The class is driven to apply higher-order cognition as they figure out why their predictions did not pan out. In the closing dialogue, the teacher ensures that students come away with clear connections to their own learning. The conclusion of Act Three reveals important truths about mathematics in the real world.
Elementary, Dear Watson! Well-crafted, rich math tasks like Array-bow of Colors, coupled with leading pedagogical practices, can play pivotal roles in student success. It occurs to me that these strategies, if enacted sensibly with students’ neurodevelopmental learning profiles in mind, have the potential to reach all students in the elementary classroom. Perhaps this neurodevelopmental lens helps us to further solve the mysteries of fine teaching. Now it is time to try Array-bow of Colors with your class so that you can see how your students solve the Skittles mystery!
Notes and Links
Math for All
The Math for All website includes resources, research, and a program description.
Three-Act Tasks
Dan Meyer, PhD, developed this strategy. His website explains the origins of the strategy and provides up-to-date resources.
“Array-bow of Colors” and Graham Fletcher’s 3-Act Tasks
Graham Fletcher’s website includes many free resources to support elementary mathematics practice.
The Array-bow of Colors Three-Act Task.
Notice and Wonder
The National Council of Teachers of Mathematics (NCTM) website contains discussion, teaching aids, and products to support this strategy.
Always Noticing and Wondering is the resource-filled website of Annie Fetter, who, along with her Math Forum colleagues, formalized the Notice and Wonder routine.
Math Talk
A web search for “math talk books” will reveal over 20 books on topics labeled Math Talk, Number Talks, and Classroom Discussions in Mathematics.
Estimation 180
Andrew Stadel developed the strategy and a set of resources to exercise this process. These two related sites contain lessons and additional resources: www.meaningfulmathmoments.com/estimation-180.html and www.estimation180.com.
C-R-A Math
The Pennsylvania Department of Education hosts this helpful presentation of Concrete-Representational-Abstract.
The contents of this blog post were developed under a grant from the Department of Education. However, those contents do not necessarily represent the policy of the Department of Education, and you should not assume endorsement by the Federal Government.
This work is licensed under CC BY-NC-SA 4.0
Math for All is a professional development program that brings general and special education teachers together to enhance their skills in
planning and adapting mathematics lessons to ensure that all students achieve high-quality learning outcomes in mathematics.
