Looking at a Student at Work

Teachers look at student work often and for many purposes. Many look individually, as a way to better understand student thinking and to inform instructional choices. Other times, looking at student work may be collaborative, such as when co-teaching, during a professional learning meeting, or as part of an instructional, curricular, or school reform decision-making process. These types of collaboration often take place after student work is completed and when students are not present. The Math for All approach combines aspects of both individual and collaborative ways of looking at student work by including planning and debriefing with colleagues and an emphasis on an observation process for looking at a student at work—attending carefully in real time to one student and their ways of learning.

Math for All professional learning is about implementing student-centered approaches for rigorous mathematics instruction. An important way it advances this is through a collaborative lesson adaptation process wherein two or more teachers—often a general education teacher and a special education teacher—work together to adapt one specific lesson or activity with one student in mind. During the adapted lesson, the teacher(s) carefully observe the student working. Afterward, the teachers reflect with colleagues on how things went for the student. This structure creates an opportunity for teachers to think deeply about one student and to more closely attend to the student’s experiences.

Teachers are encouraged to plan the lesson so it creates a context for meaningful observation of the student at work—a context in which the student reasons mathematically and communicates about mathematical ideas. One way to do this is to use a relatively open activity with a low floor and a high ceiling, as described in the two-part blog series on rich problems by Marvin Cohen and Karen Rothschild. Teachers also can promote multiple approaches for the student to engage with the activity, such as a mix of spoken language, written language, gestures, manipulatives, and visual representations like pictures and diagrams. If you have students who are multilingual learners in your classroom, creating this context may include using translanguaging as a pedagogical tool to provide access for the student and create more opportunities for the student to exhibit their thinking.

When looking at a student at work, Math for All teachers conduct low-inference observations with explicit, conscious separation of descriptive information about the student’s behavior from teacher judgments. As Rothschild et al. (2018) write in their article Learning to Look, Looking to Learn, when teachers use low-inference observations, “they notice more about student behavior, and they are better able to consider a variety of sources of that behavior” (p. 423). A simple two-column observation recording template can be used to separate what is actually observed with the senses from personal opinions and judgments. Also useful is this list of descriptive words that can support writing observation notes that are less likely to be subjective.

A related and important mindset while looking at a student at work is having a curiosity stance, as Nesta Marshall wrote in her blog on mitigating bias in mathematics instruction. This includes being self-aware and mindful of potential biases and being open to unanticipated and diverse approaches or engagement from the student. It is helpful to anticipate student engagement with the activity, but it’s critical to not let prior expectations about the student hinder potential new understandings.

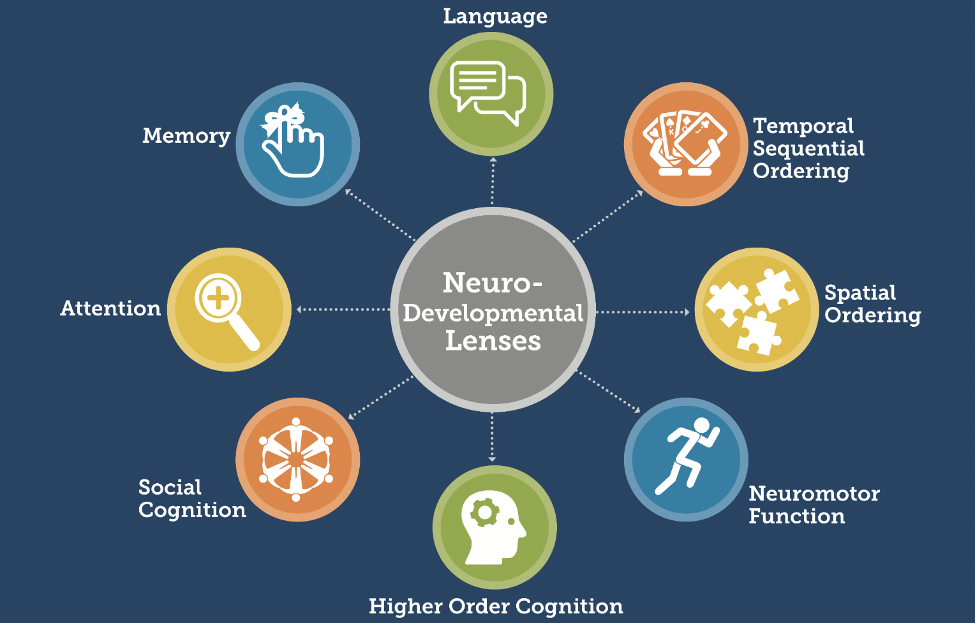
An explicit focus for Math for All teachers while planning adaptations and looking at a student at work is the student’s strengths and challenges related to one or more cognitive functions within the Neurodevelopmental Framework—such as memory, language, and higher-order thinking. When looking at the student at work during the lesson, teachers focus on what can be learned about the student’s neurodevelopmental profile and whether and how the adaptations worked for them.

Looking carefully and without bias at a student at work deepens teacher understanding of the student, and it has the potential to enrich the teacher-student relationship. It also is an opportunity for teachers to demonstrate care and to build connections with the student, and may support additional goals teachers have for their students and classrooms. For example, the process could help a teacher improve the student’s sense of belonging in mathematics or help support the student’s mathematical identity—or both.

Of course, a wider goal for teachers engaged in Math for All professional learning is that through this narrow focus on one student, teachers will be increasingly able over time to apply student-centered approaches to benefit all students. By looking at a student at work in this way, teachers practice skills and develop approaches to increase classroom inclusivity and make rich mathematics accessible for all students, so all students know they belong right there, in their classroom, with their teacher, learning important mathematics together.

References

Rothschild, K., Cohen, M., Moeller, B., Dubitsky,  B., Marshall, N., & McLeod, M. (2018). Learning to look, looking to learn. K–12 STEM Education, 4(4), 421–428.

Learning to Look 508 Compliant.pdf

The contents of this blog post were developed under a grant from the Department of Education. However, those contents do not necessarily represent the policy of the Department of Education, and you should not assume endorsement by the Federal Government.

This work is licensed under CC BY-NC-SA 4.0