Parallel Pathways: Design Thinking, STEAM, and Math for All
By Peter Tierney-Fife, Andrea Brothman, and Karen Rothschild

Removing barriers to learning is fundamental to our work as educators. One way to do this is to approach lesson design through a multidisciplinary lens, taking natural advantage of the variety of skills, dispositions, and individual levels of interests inherent in each one. Planning lessons, units or courses specifically from a STEAM (science, technology, engineering, the arts, and math) approach can open up learning experiences to a range of learners because of both content-driven intersection points and the interdisciplinary impetus for inquiry and investigation.
According to the Institute for Arts Integration and STEAM, “STEAM Education is an approach to learning that uses Science, Technology, Engineering, the Arts and Mathematics as access points for guiding student inquiry, dialogue, and critical thinking.” It is a way to create holistic lessons and projects that integrate the subject matter from the various disciplines as well as their different approaches to problem solving. Because it offers students a variety of ways of thinking, and provides opportunities to approach problems in multiple ways, STEAM education aligns well with Math for All. We think it’s a useful thing to try in our classrooms.
Below is one example of what that might look like.
Ms. Lopez, a Math for All teacher, is thinking about the upcoming school-wide beautification project. She wonders about ways her grade can contribute, knowing how much they enjoy this annual effort. She would like to integrate art and math learning, yet her ideas are amorphous and she knows she will have to develop and try out different ones to give form to the project. She decides that Design Thinking—a collaborative and iterative problem-solving process—could be a helpful tool to move her thinking forward. Ms. Lopez decides to engage all the teachers in the grade in her planning efforts.
As the graphic shows, Math for All’s Lesson Adaptation Cycle and the design thinking process have several features in common. They both
- present a series of steps that rely on inquiry, creativity, empathy, and curiosity;
- acknowledge that solutions are always in development and refined over time; and
- inherently value collaboration and reflection.
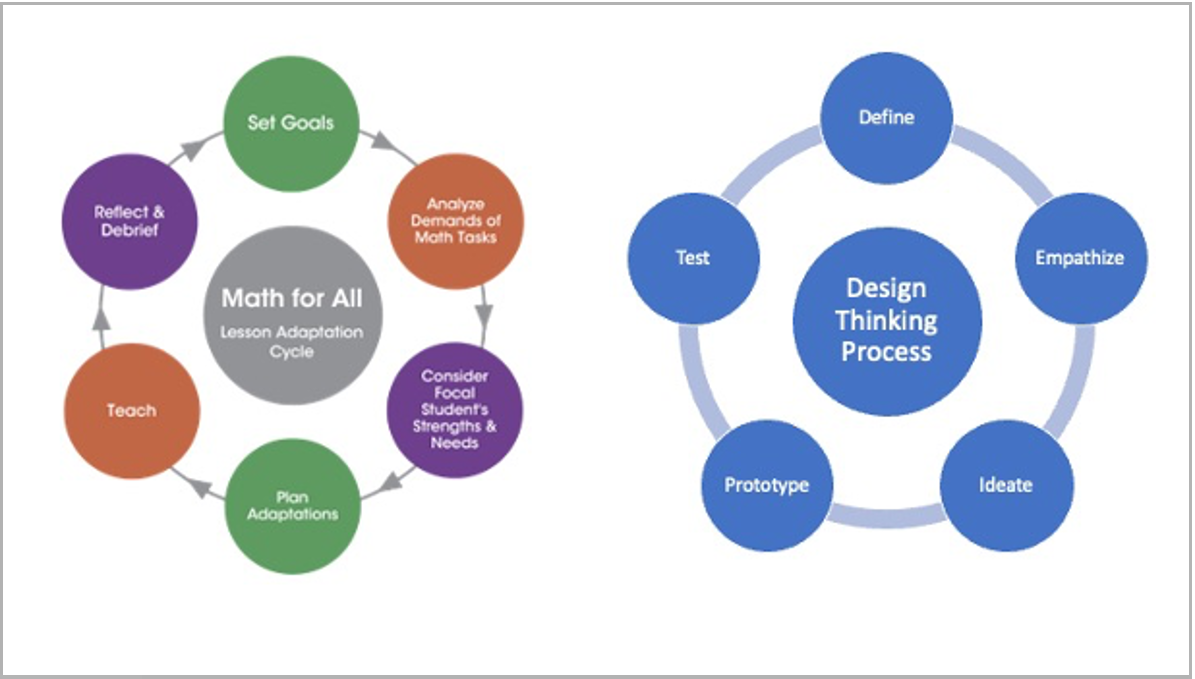
The process described below illustrates the shared features of these two approaches and how design thinking helps Ms. Lopez and her colleagues create a project prototype.
Step 1: Define Goals
Like the Math for All lesson adaptation cycle, the first step in Design Thinking is to be explicit about goals. At this stage of the design process, the teachers’ goals are still quite general—to design a school beautification project that offers opportunities for students to engage in problem solving in two of the STEAM disciplines, art and math.
Step 2: Gather Information
There are several kinds of information to investigate in this step. First, it’s essential to determine student interests and strengths with respect to the project as well as the interests of the school community. The team also needs to determine the resources the school and the community might be able to provide. This step is a more open version of discovering the demands of the task in Math for All in that the effort allows teachers to identify the opportunities and constraints of an activity in relation to those it will serve.
Ms. Lopez and her team begin by announcing the beautification project to their classes and getting input from students about their interests in both art and math. They ask questions such as:
- What makes a beautiful environment?
- What types of beautiful spaces do you like spending time in?
- What ideas do you have for a beautification project?
- What artistic materials do you like using?
- What art tools and math tools are you curious about?
- What do you like and what is hard for you about working on group projects?
- Who else in our community might be interested in helping with this project?
Through this conversation, the teachers are surprised to learn that the students are already imagining projects like a mural in the lobby and raised garden beds at the front of the school. They also learn that a few students are in the after-school art club and have recently completed a mosaic project.
Step 3: Brainstorm and Prototype
The purpose of this step is to examine the data gathered in the previous step and, with the goals in mind, generate implementation ideas for the project. This is similar to the thinking that Math for All teachers do about a focal student’s strengths and challenges before adapting a lesson.
In our example, the teachers identify key takeaways from their research and begin brainstorming. They jot down as many potential “prototype” project ideas that combine art and math as they can. The teachers ask themselves:
- Where do the intersections between our goals and the project opportunity seem strongest or make most sense to consider further?
- How do our students’ interests and strengths connect with the grade’s mathematics standards and our art goals for this project?
- What kinds of support might my students need in order to meet the goals?
Ms. Lopez and her colleagues talk through the pros and cons of various project ideas and settle on moving forward with a mural for the beautification project. Students expressed interest in painting and wondered about the process artists use to create wall-size murals from table-sized drawings. The teachers see that making a mural could immerse students in an authentic project that involves artistic creativity and provides opportunities to learn about area, ratio and proportion, geometry, and measurement.
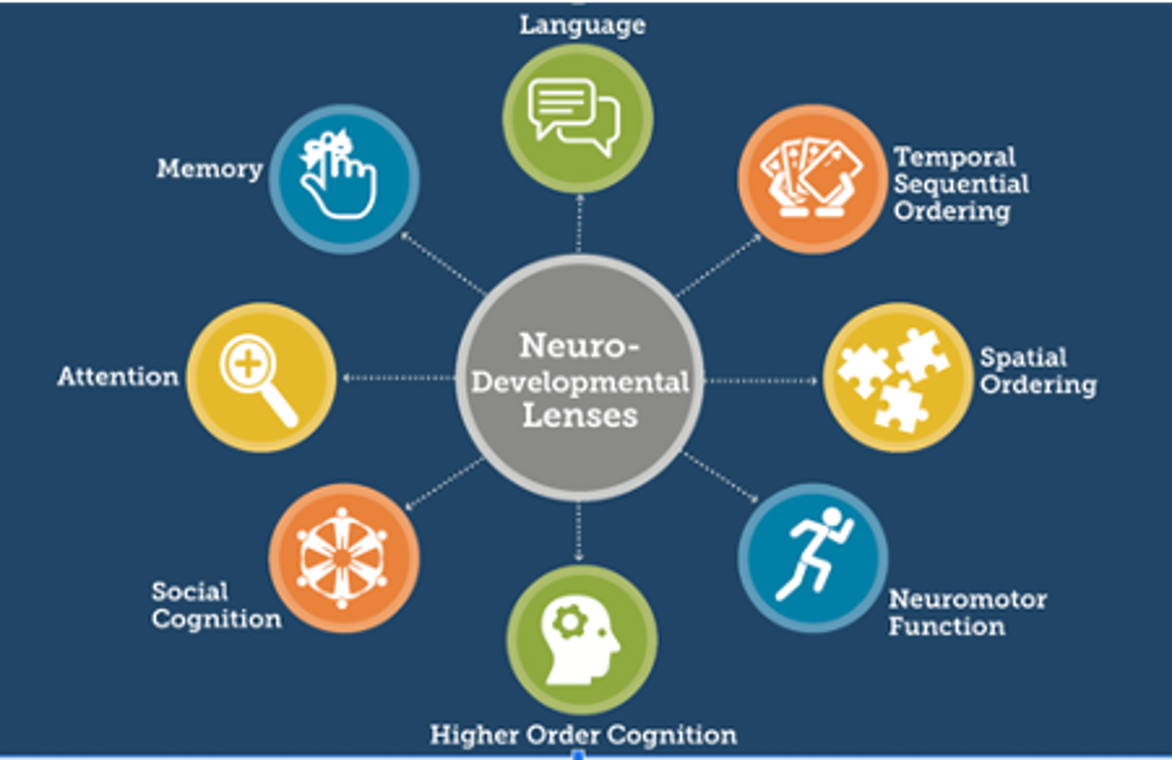
Together the teachers write lesson plans for creating the mural and integrating specific art and math concepts. Using the Math for All Neurodevelopmental Framework they consider the demands of the different tasks in the development of the mural and adapt them to take advantage of their students’ strengths and mitigate their students’ challenges in both the artistic and mathematical aspects of the project. They recognize and celebrate the fact that combining art and math gives students a variety of entry points through which to show their strengths.
Step 4: Implement and Reflect
Both Math for All and Design Thinking consider any implementation of a lesson or a project as a kind of action research project. A design thinking approach is iterative in that resulting products are continually refined. Similarly, the Math for All Lesson Adaptation Cycle is recursive—teachers closely observe what students do in a lesson and reflect on the elements of their plans that led to student achievement of their goals as well as what could be improved for the next implementation.
In our example, Ms. Lopez and her colleagues implement their lesson plans, make low-inference observations of their students as they work, and collect formative data on what the students learned about the specific art and math goals. When the project ends, the teachers sit down and reflect on their lessons and note the changes to make for next time.
Design Thinking, STEAM, and Math for All
STEAM Education, Design Thinking, and Math for All are mutually supportive. Design Thinking and Math for All both involve a development process that focuses on goals, finding creative ways to plan for reaching those goals, and reflecting on implementations with an eye toward improvement. In the same way that the Math for All Lesson Adaptation Process views students’ strengths and challenges as equally critical considerations for lesson adaptation, STEAM lessons support students by providing multiple entry points for content exploration that can build on student interests, highlight strengths, and create authentic contexts for students to work on mathematical challenges in pursuit of non-mathematical goals, such as the mathematical aspects of art. All three frameworks stress the advantages of collaborative planning and reflection. They all emphasize examining a variety of solution strategies and encourage experimentation with ideas and learning from attempts that don’t work.
Celebrate STEAM with your students by trying something new with them. Maybe what you try will be worth adapting further to make it a regular feature of your mathematics instruction.
The contents of this blog post were developed under a grant from the Department of Education. However, those contents do not necessarily represent the policy of the Department of Education, and you should not assume endorsement by the Federal Government.
This work is licensed under CC BY-NC-SA 4.0
Math for All is a professional development program that brings general and special education teachers together to enhance their skills in
planning and adapting mathematics lessons to ensure that all students achieve high-quality learning outcomes in mathematics.
